Liczby zespolone w demodulacji sygnałów radiowych
Opublikowano: 22.10.2024
Liczby rzeczywiste są obecne niemal wszędzie wokół nas. Używamy ich do całego szeregu rzeczy: długość drogi, napięcie w gniazdku, czy prędkość samochodu to wszystko przykłady zastosowań liczb rzeczywistych. Liczby te tworzą fundament dla wielu dziedzin nauki, od matematyki przez fizykę, aż po inżynierię.
Jednak gdy pochylimy się nad bardziej zaawansowanymi technikami jak np. modulacja i demodulacja sygnałów (którą w bardzo podstawowym zakresie zajmę się w tym artykule), liczby rzeczywiste przestają być wystarczające.
W tym artykule zaprezentuję zastosowanie liczb zespolonych do demodulacji sygnału radiowego AM, który polega na kodowaniu sygnału informacyjnego wykorzystując chwilowe zmiany amplitudy.
Ale zaraz zaraz! Przecież sygnał AM jak najbardziej można zapisać wykorzystując tylko i wyłacznie liczby rzeczywiste, dla czego zatem męczyć sie i dodawać liczby urojone do zestawu?
Matematycznie możemy opisać taki sygnał jako:
\( s(t) = [A + m(t)] \cdot \cos(2 \pi f_c t) \)
Gdzie:
- \( A \) to stała reprezentująca nośną,
- \( m(t) \) to sygnał informacyjny,
- \( f_c \) to częstotliwość nośna.
Ten wzór pokazuje, że sygnał AM można opisać za pomocą liczb rzeczywistych, ponieważ składa się wyłącznie z rzeczywistego cosinusa, a informacja o amplitudzie jest również rzeczywista. I faktycznie, w prostych systemach analogowych można przetwarzać taki sygnał bez użycia liczb zespolonych
Dlaczego jednak używamy liczb zespolonych?
Choć liczby rzeczywiste mogą wystarczyć, liczby zespolone dają nam znacznie większą elastyczność i efektywność w przetwarzaniu sygnałów, szczególnie w cyfrowych systemach radiowych, takich jak SDR (Software-Defined Radio).
Jednymi z popularniejszych radii SDR są np. RTL-SDR czy SDRPlay.
Jedną z najważniejszych zalet korzystania z liczb zespolonych jest to, że pozwalają nam reprezentować zarówno amplitudę, jak i fazę sygnału w bardziej bezpośredni i wygodny sposób. Liczby zespolone składają się z części rzeczywistej (I, In-phase) i urojonej (Q, Quadrature). Dzięki tej reprezentacji można łatwo manipulować sygnałem w domenie czasu i częstotliwości.
Sygnał I/Q w radiu SDR
Gdy korzystamy z radia SDR, często nie otrzymujemy sygnału w postaci prostego, rzeczywistego sinusa. Zamiast tego, SDR zwraca sygnał I/Q – zespoloną reprezentację sygnału:
\( s_{\text{complex}}(t) = I(t) + jQ(t) \)
- \( I(t) \) to składowa "In-phase", która jest proporcjonalna do rzeczywistego sygnału nośnego.
- \( Q(t) \) to składowa "Quadrature", która odpowiada sygnałowi przesuniętemu o 90 stopni względem I(t).
Dzięki tej zespolonej reprezentacji możemy dokonywać bardziej zaawansowanych operacji na sygnale, np. przesunięcia częstotliwości czy filtracji w domenie częstotliwości, bez potrzeby skomplikowanych operacji trygonometrycznych.
Część praktyczna
W ten sposób dochodzimy do kluczowego pytania: jak wygląda przetwarzanie sygnału radiowego przy użyciu liczb zespolonych? Jak dzięki temu możemy przeprowadzić demodulację sygnału AM?
W pierwszej kolejności musimy nagrać próbki sygnału IQ by miec na czym pracować.
Ja wykorzystałem radio SDR podpięte do laptopa i program SDR++ by nagrać baseband (sygnał IQ).
Kolejnym krokiem będzie napisanie kodu który odzwierciedli wspomnianą powyżej teorię.
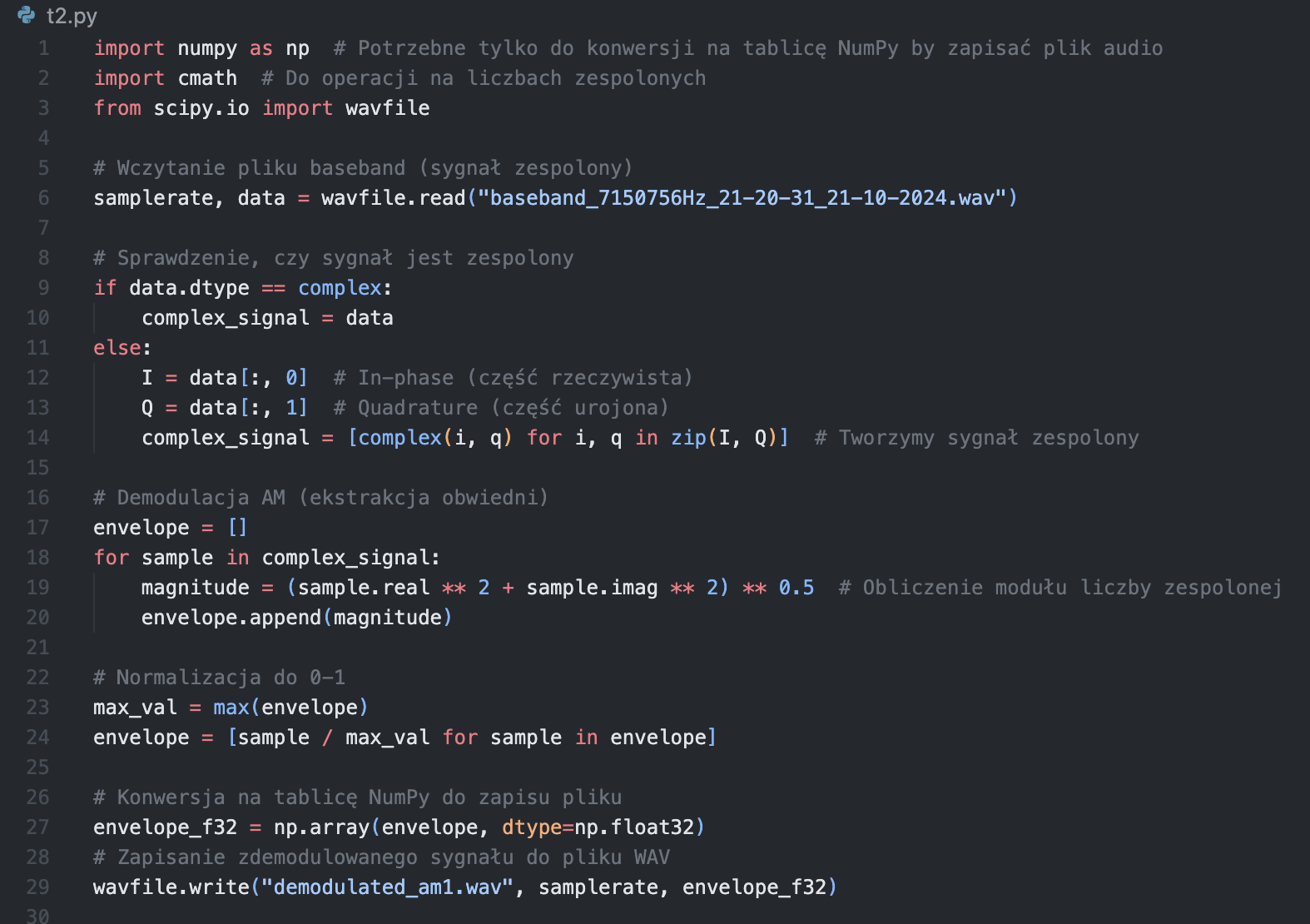
W poniższym przykładzie pokażę, jak za pomocą Python'a można wczytać sygnał I/Q z radia SDR, a następnie zdemodulować przy pomocy liczb zespolonych.
Przykład jest bardzo uproszczony i brakuje w nim filtrów, przesuwania sygnału w domenie częstotliwości, czy szerokości pasma w związku z czym jako efekt uzyskamy plik gdzie wszystkie sygnały będą wymieszane jednak powinno być słychać najmocniejszą stację i wystarczy to do prezentacji działania.
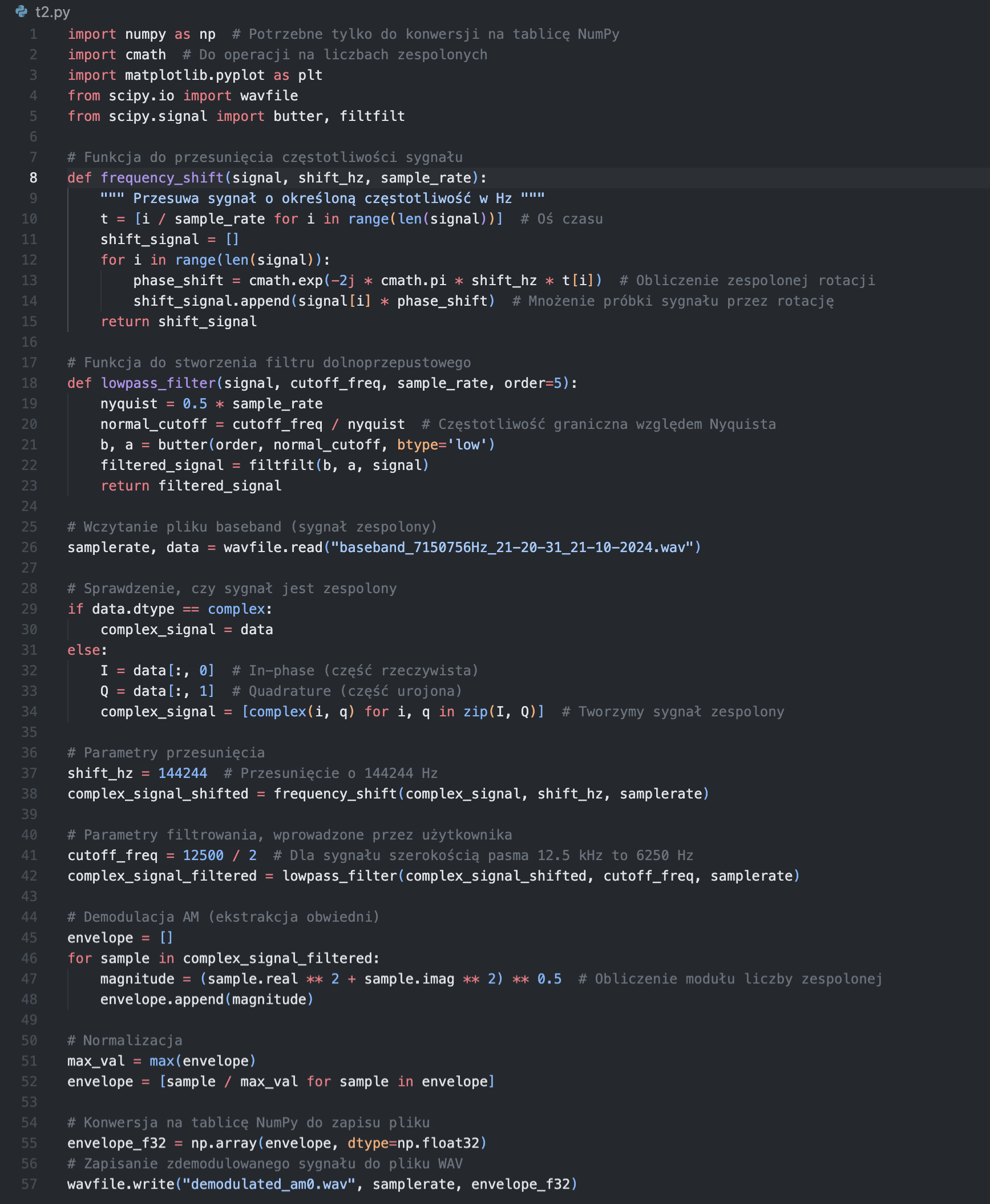
Na koniec dodam jeszcze przykład bardziej zaawansowanej wersj która pozwala przesunąć sygnał na porządaną częstotliwość oraz ustawić szerokość pasma więc nie słyszymy innych niechcianych stacji. Nagrany przeze mnie wczesniej sygnał IQ jest wycentroway na 7150756Hz, a chcę posłuchaćstacji na 7295000Hz dla tego przesuwamy tu sygnał o 7295000 - 7150756 = 144244Hz.
Źródła:
https://pl.wikipedia.org/wiki/Modulacja_amplitudy
https://wiki.gnuradio.org/index.php/IQ_Complex_Tutorial


